Over the last week I’ve wanted to build a project using amazon EC2, and I had an idea based off our office ping pong tournament: what if I built a site that would track rankings over time to see how players were doing? It seemed pretty novel, the site wasn’t too hard to build. I used Ruby on Rails for the backend, made two table, one for employees and another for games played, and used d3 to build a graph to show peoples work over time. The only issue I had which took up most of my time was building the algorithm, which proved to be rather difficult.
The Problem
In order to graph everyone’s ranks, I wanted to use a scalar value to represent how people were doing. I ended up creating a list of constraints, that are as follows:
- It should range over 1 to 1000, averaging around 500
- Players who win against better players (unexpected win) should receive a higher bonus
- Players who beat worse players (expected) should win less
- These changes from new score to old score (delta) should scale based on how good they are
- As players combined average moved away from 500, they should gain or lose less points (this would later be changed from an explicit requirement to an implicit one, as the former was too difficult to implement)
One way to this of this problem is to consider the graph below. If each score is the same, players would gain and lose the same amount of points; a value we’ll refer to as n (and in my project n = 10). If an unexpected outcome occurs (winner has less points than the loser), as the score difference increases they would be awarded and decremented more points appropriately. As we see expected outcomes occur with higher point differences, they’d each gain and lost points as expected, but the change in points to their scores (delta) would be lower.
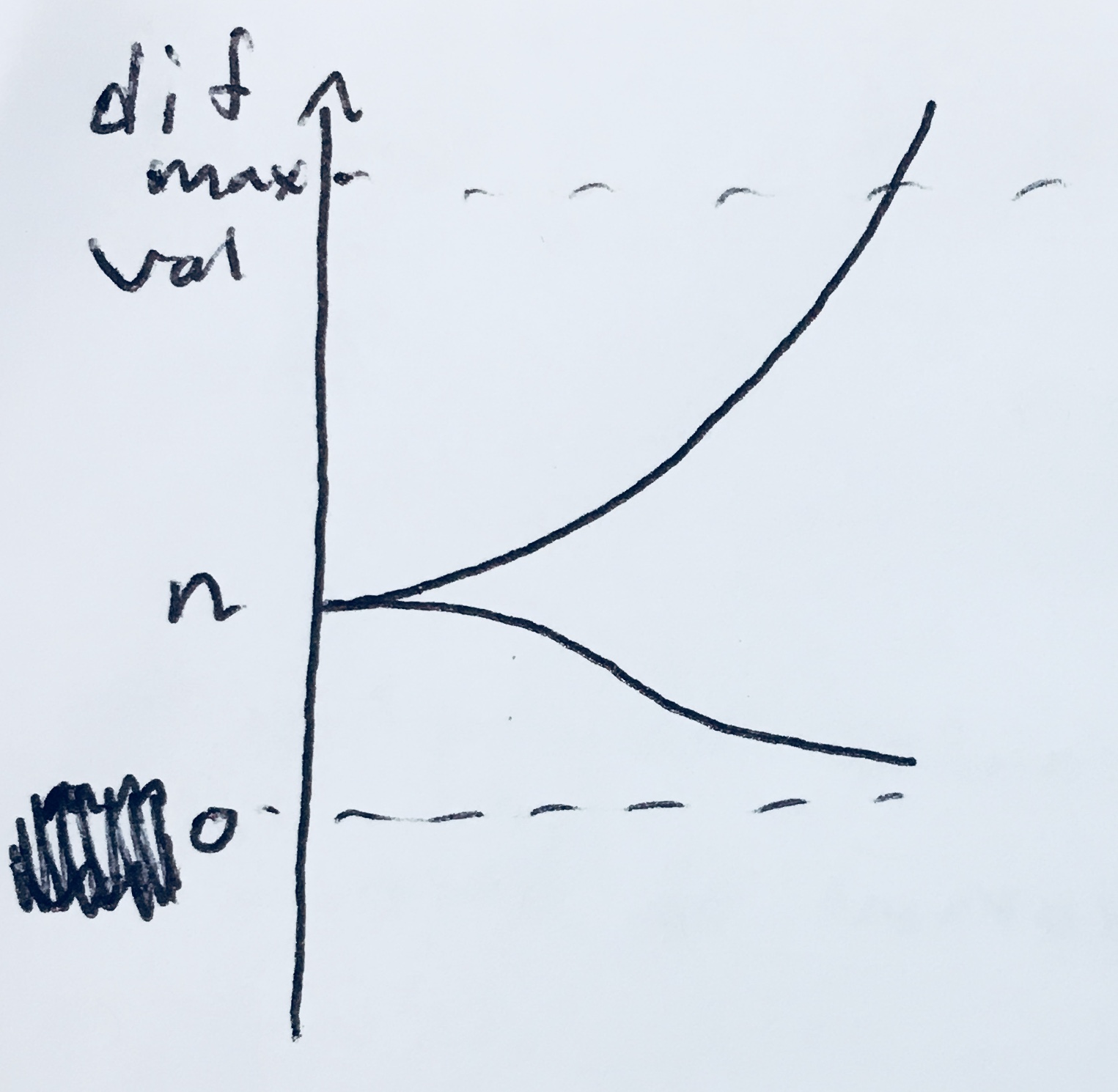
I ended up trying to use two algorithms I’ll mention here, two because one of them explicitly deals with the increasing average problem, and one implicitly deals with it (but works overall much better).
Logorithm Reminder
For anyone who might try to implement this problem, since remarkably many languages don’t support different bases and I used logarithms a bit in the algorithms, I’d like to remind you that
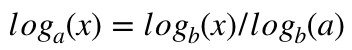
Algorithm 1: explicit attention to the increasing average problem (but fundamentally broken)
So here we can view the algorithm as a whole as follows in ruby code:
% assign l and w ranks appropriately
if (w > l) % expected
windiff = 1/log(abs(l-w));
else % unexpected
windiff = log(max(abs(l-w),1.5));
end
frommid = (500/(abs(abs(l-w)/2 - 500)));
delta = windiff * frommid;
new_winner_rank = min(w.rank + delta, 1000)
new_loser_rank = max(l.rank - delta, 1)
Where l is the rank of the loser and w is the rank of the winner. Here we see two main equations and an if-else statement. The statement is used to determine which algorithm to use, based on whether the outcome was expected or not. Additionally the if-else statement houses the windiff, which is the portion of the calculation that is considering the difference between their ranks. The log increases gradually as we grow farther apart, and the inverse log is used for expected outcomes to reduce the size of delta when their values are far apart. The max statement is used so that in cases where the values are equal it doesn’t all go to 0, but rather the delta would be an approximately constant value.
Secondly we have the frommid equation, which checks how far from the midpoint (500pts) the players average rank is. As they grow farther from the center, the value becomes farther away from 500/500, creating a smaller value. We lastly multiply these together to get our delta, and then add or subtract this from the final ranks before updating the table. In theory this should be good, however we encounter scaling problems as it’ll often increase too quickly or not quickly enough as the score goes up. I believe this could be a useable solution by adding exponents to mitigate or amplify their effect, however I wasn’t able to find a solution.
Implicit decrease algorithm (and the one in production)
Secondly we come to this algorithm; the one I’d recommend using. It’s a bit simpler than the first, mainly in that it doesn’t have the ‘frommid’ equation anymore. We know as the two values both increase or decrease, they will implicitly have smaller deltas since the difference between the two values will always be smaller (i.e. if they’re both larger than 500 then the max diff can only be < 500, where as if we use the whole range it can be up to a difference of 1000). Again in matlab code the algorithm I used works as follows, where I had an n of 10 (n being the base change for if both values equaled each other):
dif = abs(w - l);
if (w < l) % unexpected
delta = 10 + (1/1250)*dif^2;
else % expected
delta = min(10/log10(dif), 10);
end
new_winner_rank = min(w.rank + delta, 1000)
new_loser_rank = max(l.rank - delta, 1)
Here we see a much more elegant solution. For unexpected solutions, as the difference increases we see it increase over the full possibly range of values, and it does so gradually due to the 1/1250 constant. If the value is expected, we either take the maximum value of 10, or we take the reduced value of 10/log10(diff), which will decrease slowly as the difference becomes larger. I’d like to mention the log base 10 was specifically chosen to match the n value of 10. If you want your scale to move more quickly, then I’d recommend using a larger n value, and thus having a larger base of value n as well.